Using Bayesian Inference for Uncertainty Quantification of Rheology of Thermal Greases

Predicting flow behavior of DOWSIL TC-5550 thermal grease with Bayesian Inference models and quantifying parameter uncertainties

Technical skills: Python (NumPy, Pandas, emcee, NumPyro), Linux, Bayesian Modeling, Markov-Chain Monte Carlo Algorithms

Continuing from my previous work on neural networks with Dr. Ivan Christov in the Transport: Modeling, Numerics & Theory Lab, my next project within the research was to quantify the uncertainties of the parameters in the rheological models that we were evaluating. For my contributions in novel research, I was recognized as an H. William Bottomley Scholar by School of Mechanical Engineering at Purdue and was awarded a research scholarship.

My work in Spring 2024 largely focused on the Nonlinear-elasto-visco-plastic (NEVP) model of DOWSIL TC-5550 Thermal grease, and using Bayesian Modeling and Inference to calculate the future/posterior statistical distributions of the five parameters that define the grease’s behavior in the NEVP model. The poster I made to summarize my research can be found below.

The first month of research was focused on learning the foundations of Bayesian Modeling and Inference using conditional probabilities, and familiarizing with emcee, a Python module that implements a specific algorithm of the Markov-Chain Monte Carlo (MCMC) process. Using emcee, posterior probabilities and uncertainty spreads can be calculated of the parameters. There was data from five different shear rates for the TC-5550 grease. To evaluate the performance of emcee, the Bayesian Inference was performed on data from one shear rate.

The next couple of months were focused on fine-tuning the algorithm parameters for one shear rate, and then expanding the Bayesian Inference to all the shear rates. To evaluate emcee’s performance further, Pranay Nagrani, a PhD candidate working with Dr. Christov, performed Bayesian Inference on the experimental data using PyMC3. I was also able to gauge the effectiveness of the emcee module by applying interpolation and extrapolation of different shear rates.

Posterior Joint Probability Distributions of NEVP Model Parameters, different colors indicating different shear rates on the left and the global probability distributions for all shear rates on the right

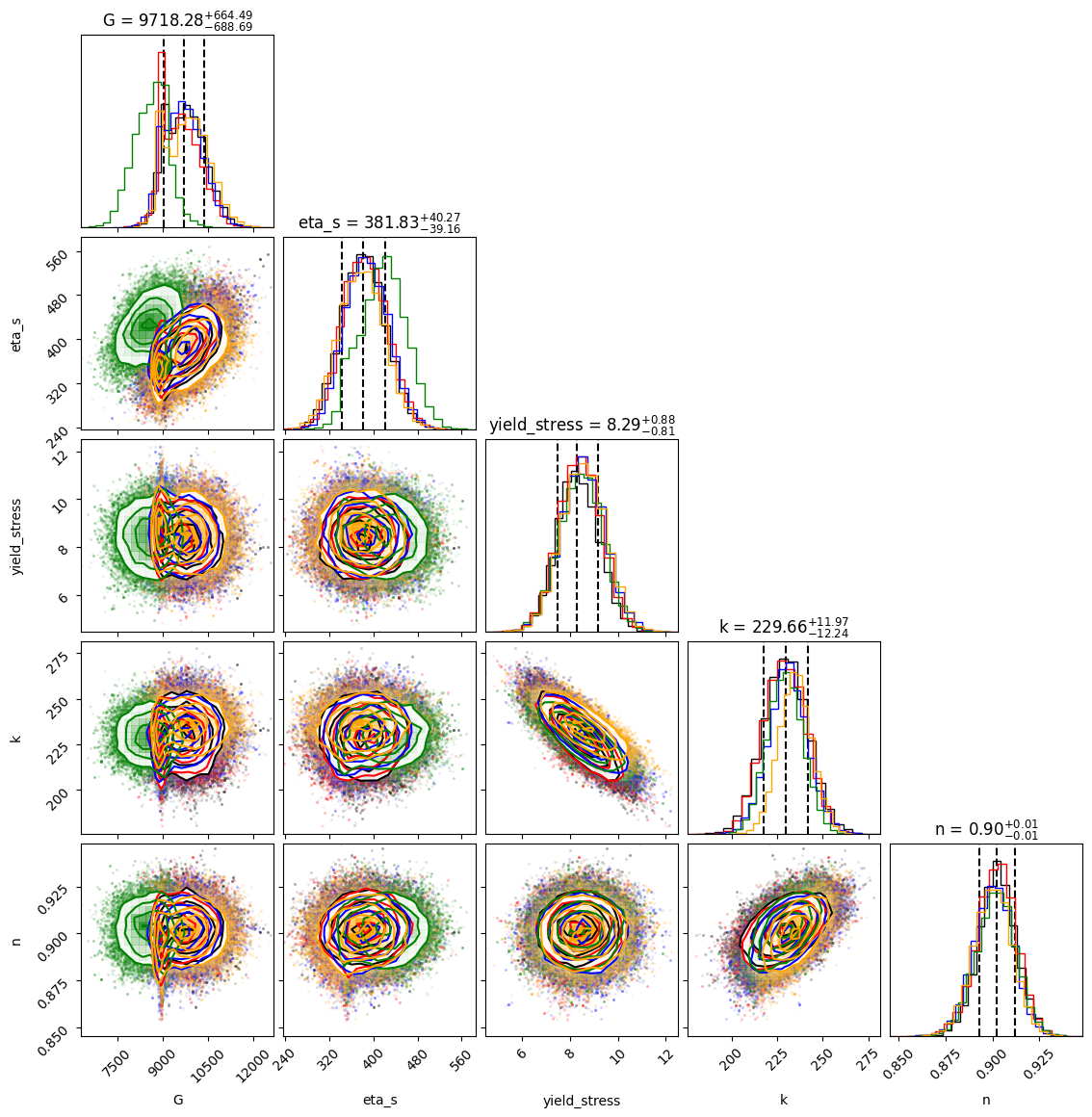
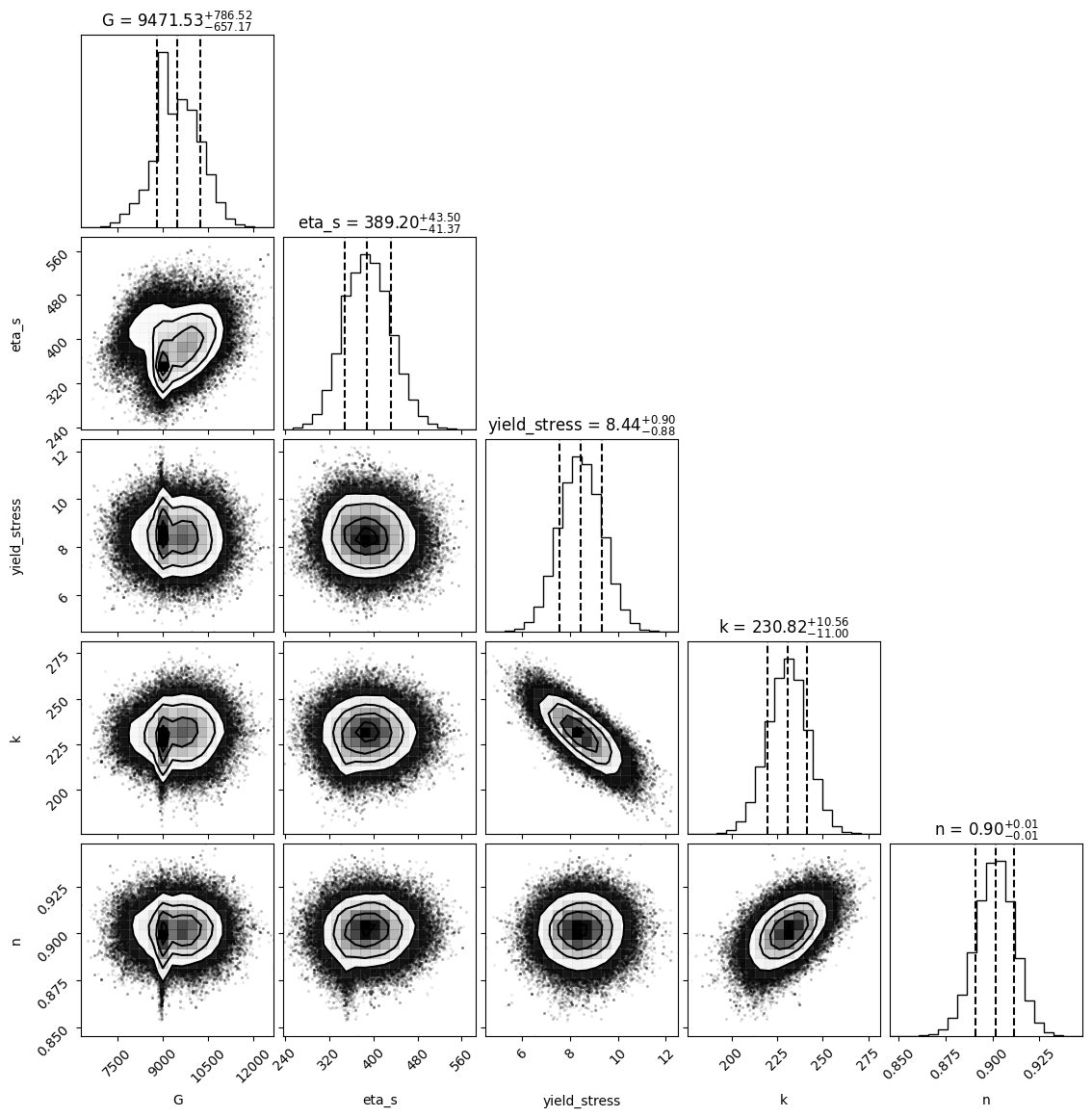
Most of the work went into fine-tuning the parameters of the MCMC algorithm, such as:

  • Number of MCMC chains (known as walkers)
  • Number of iterations
  • Ranges and type of prior distributions for parameters in NEVP model
  • Ways to implement multiple shear rates
  • Method of integrating ODEs effectively within MCMC code

I hope to continue working closely with Dr. Ivan Christov and Pranay Nagrani in the near future to produce more concrete results for this research.